博弈论(Game Theory)又称为对策论或赛局理论,是经济学的一个分支,也是运筹学的一个重要学科,该理论专门研究多个独立个体之间的竞争行为(对抗行为)。

1944年,约翰·冯·诺伊曼(John von Neumann)与奥斯卡·摩根斯坦(Oskar Morgenstern)合作发表了《博弈论与经济行为》(Theory of Games and Economic Behavior),一举奠定博弈论体系的基础。

约翰·冯·诺伊曼(John von Neumann)
约翰·冯·诺伊曼是出生于匈牙利的美国籍犹太人数学家,现代电子计算机与博弈论的重要创始人,被称为“现代计算机之父”和“博弈论之父”。他还在更多领域作出了划时代的贡献。

Theory of Games and Economic Behavior,60th anniversary edition, 2004
在普林斯顿大学出版社发行60周年纪念版的介绍中,《博弈论与经济行为》被描述为“现代博弈论所基于的经典著作”。
如果难以咽下经典著作,这里推荐博弈论入门图书《策略思维:商界、政界及日常生活中的策略竞争》(Thinking Strategically: The Competitive Edge in Business, Politics, and Everyday Life)。

THINKING STRATEGICALLY by Avinash K.Dixit、Barry J.Nalebuff
《策略思维》是面向零专业基础的读者了解、学习博弈论的经典入门读物,两位作者分别是耶鲁大学和普林斯顿大学的教授,同时也是有名的经济学家。
这本书完全以讲故事和案例的形式为我们展示了博弈论策略思维的应用之道。作者以商界、政界以及日常生活中的生动例子为引入,为我们作了一场博弈论的趣味普及:
- 策略思维的基本概念:通过商界、体育、政治等各领域的例子,介绍博弈论策略思维工具的基本概念,包括博弈的分类、策略思维的基本运作法则等。
- 策略思维的关键要点:进一步阐述博弈论策略思维工具的关键运用技巧,包括承诺、威胁、许诺、警告等各类策略行动的操作要点。
策略思维的具体应用:再次回归案例,通过讨价还价、投票选举、边缘政策以及激励设计等常见实操例子,探讨博弈论策略思维工具的具体应用,深化读者理解。
决策的相互依存性:只有在双方一致选择单独看来不那么好的策略的时候,才会取得对于双方都更好的结果。
第1部分结语:
博弈是一种策略的相互依存状况:你的选择(即策略)将会得到什么结果,取决于另一个或者另一群有目的的行动者的选择。处于一个博弈中的决策者称为参与者,而他们的选择称为行动。一个博弈当中的参与者的利益可能严格对立,一人所得永远等于另一人所失。这样的博弈称为零和博弈。不过,更常见的情况是,既有共同利益,也有利益冲突,从而可能出现导致共同受益或者共同受害的策略组合。但是,我们通常还是会把这个博弈当中的其他参与者称为一方的对手。
一个博弈的行动可能是相继进行,也可能是同时进行。在相继行动的博弈里,存在一条线性思维链:假如我这么做,我的对手可以那么做,反过来我应该这样应对…… 这种博弈通过描绘博弈树进行研究。只要遵循法则1:向前展望,倒后推理,就能找出最佳行动方式。
而在同时行动的博弈中,存在一个逻辑循环的推理过程:我认为他认为我认为…… 这个循环必须解开,一方必须看穿对手的行动,哪怕他在行动的时候并不知道这是怎么一回事。要想解开这么一种博弈,可以建立一张图,这张图能显示所有可能想像得到的策略组合将会相应产生什么结果。然后按照下列步骤进行分析。
首先看参与各方有没有优势策略,优势策略意味着,无论对手采取什么策略,这一策略都将胜过其他任何策略。这就引出法则2:假如你有一个优势策略,请照办。假如你没有优势策略,但你的对手有,那么,尽管认定他一定会照办吧,然后相应选择你自己的最佳策略。
接着,假如没有一方拥有优势策略,那就看看有没有人拥有一个劣势策略,劣势策略意味着无论对手采取什么策略,这一策略都将逊于其他任何策略。如果有,请遵循法则3:剔除劣势策略,不予考虑。如此一步一步做下去。假如在这么做的过程当中,在简化之后的博弈里出现了一个优势策略,应该采用这个优势策略。假如这个过程以一个独一无二的结果告终,那就意味着你找到了参与者的行动法则以及这个博弈的结果。即便这个过程可能不会导出一个独一无二的结果,这么做也可以缩小整个博弈的规模,使其变得更加容易控制。最后,假如既没有优势策略,又没有劣势策略,又或者这个博弈已经经过第二步进行了最大限度的简化,那么,请遵循法则4:寻找这个博弈的均衡,即一对策略,按照这对策略做,各个参与者的行动都是对对方行动的最佳回应。假如存在一个这样的独一无二的均衡,我们就有许多很好的证据证明为什么所有参与者都应该选择这个均衡。假如存在许多这样的均衡,你就需要用一个普遍认同的法则或者惯例做出取舍。假如并不存在这样的均衡,这通常意味着一切有规则可循的行为都有可能被对方加以利用,这时候你需要将你的策略混合运用。
在实践当中,博弈可能包含一些相继行动过程,也可能包含一些同时行动过程,因此须将上述技巧综合起来,灵活运用,思考和决定自己的最佳行动应该是什么。
一、博弈的类型

囚徒困境(prisoner’s dilemma)
合作博弈(Cooperative Game)和非合作博弈(Bon-Cooperative Game)
对于合作博弈,存在某种外部约束力,使得“背叛”的行为会受到这种外部约束力的惩罚。如商业合同。
对于非合作博弈,没有上述这种外部约束力,对“背叛”的惩罚只能依靠博弈过程的其它参与者。
同时博弈(Simultaneous Game)也称作静态博弈和顺序博弈(Sequential Game)也称作动态博弈。
同时博弈是指博弈的任何一个参与者在选择自己的行为之前,并不知道其它参与者的行为信息。如石头剪刀布游戏。
顺序博弈是指参与者的动作有时间上的先后,并且后一个执行动作的博弈者可以看到其他博弈者之前的动作,然后根据别人的动作,思考自己的行为。如绝大部分棋牌类游戏。
零和博弈(Zero-Sum Game)和非零和博弈(Non-Zero-Sum Game)
零和博弈是在博弈结束之后,参与各方的利益总和为常量。如大多数棋类游戏。
非零和博弈是 在博弈结束之后,参与各方的利益总和为变量。如囚徒困境(Prisoner's Dilemma)。
非重复博弈(Non-Repeated Game)和重复博弈(Repeated Game)
非重复博弈有时也称作“单次博弈”;相应的,“重复博弈”也被称作“多次博弈”。重复博弈还可以进一步细分为有限重复博弈(Finite Repeated Game,重复次数确定的博弈)与无限重复博弈(Infinite Repeated Game,重复次数不确定的博弈)。
二、收益矩阵和决策树
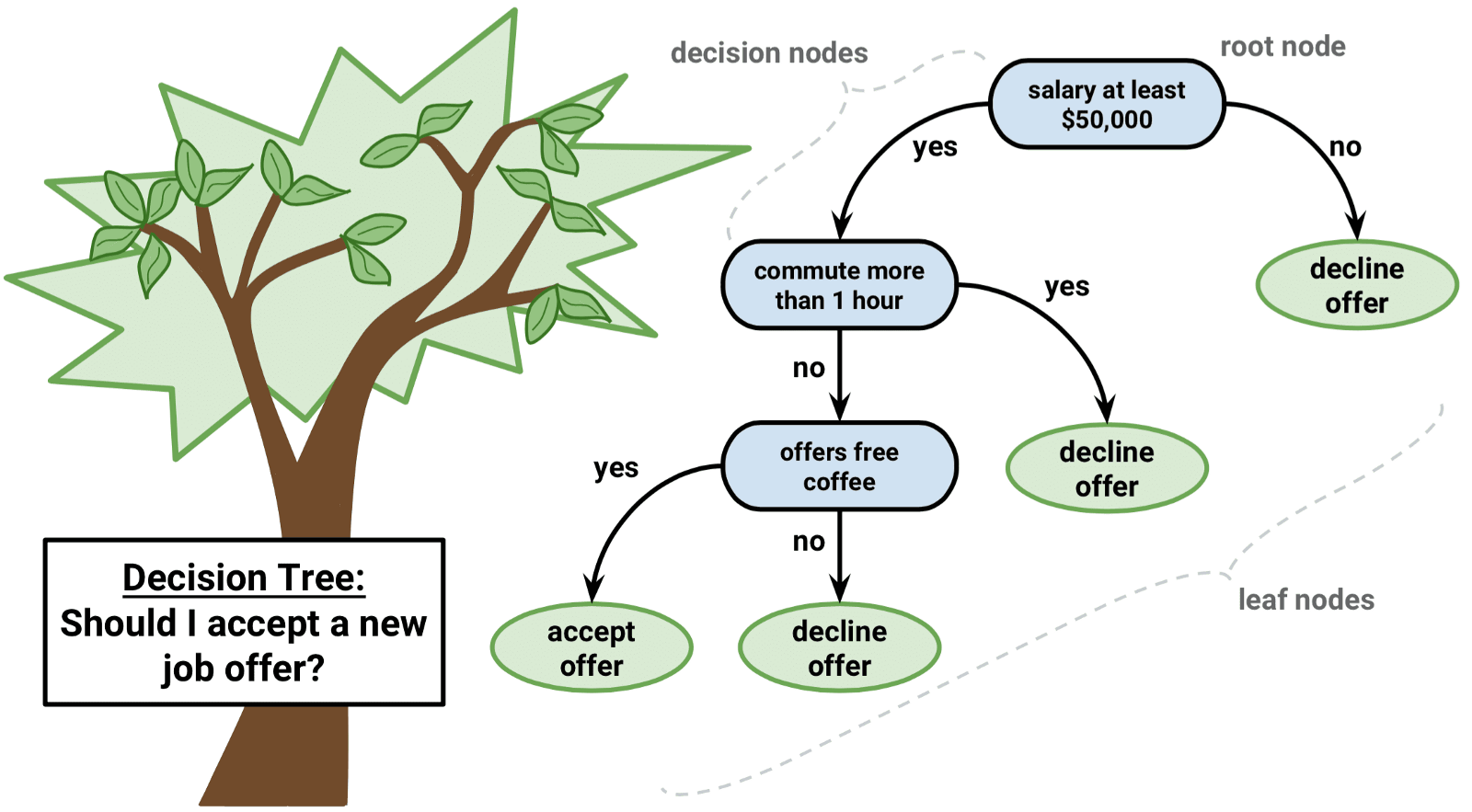
决策树(Decision Tree)
收益矩阵(Payoff Matrix)和决策树(Decision Tree)是更直观地描述博弈过程,并帮你看清各方的利弊得失的两个工具。收益矩阵也称作普通形式(Normal-Form);把决策树称作扩展形式(Extensive-Form)。
收益矩阵通常用来描述双人同时博弈,通常的惯例是把自己这方的策略写在表格左边,把对方的策略写在表格上边。
决策树既可以用来描述同时博弈,也可以用来描述顺序博弈。
三、策略和策略集合

决策的每个步骤叫决策选项(Move),所有决策选项的总和叫策略(Strategy),所有可能的策略,构成了策略集合(Strategy Set)。策略集合分为有限策略集合和无限策略集合。
四、纯策略和混合策略
在实际博弈时,如果你总是固定选择策略集合中的某一个策略,这种情况称之为纯策略(Pure Strategy)。
如果你在博弈时,总是随机选择策略集合中的某几个策略,这种情况称之为混合策略(Mixed Strategy)。
如果某个混合策略包含了策略集合中的每一个元素,称之为完全混合策略(Totally Mixed Strategy)。
五、支配策略(优势策略)
支配策略又称优势策略。如果某个策略能够支配所有其它策略,那么它就是支配策略(优势策略)(Dominant Strategy)。
有时候会把支配策略进一步细分为强支配策略(Strictly Dominant Strategy)和弱支配策略(Weakly Dominant Strategy)。
对于前者,它在任何情况下都比其它策略更好;对于后者,它在某些情况下比其它策略更好,某些情况下与其它策略一样好。
制胜策略(Winning Strategy)也称必胜策略,它通常只用于零和博弈,指的是只要你采用这个策略(不论对方如何应对),你总是赢。
制胜策略肯定是支配策略;但支配策略不一定是制胜策略。
如何发现支配策略,一个比较简单的做法是:逐步删除被支配的策略(Iterated Elimination of Strictly Dominated Strategies,简称 IESDS),剩下该博弈的纳什均衡点。
六、最小最大定理
最小最大(Minimax)定理:最小化最大损失,该定理及算法最早由冯·诺依曼在《博弈论与经济行为》一书中提出。
七、反向归纳法
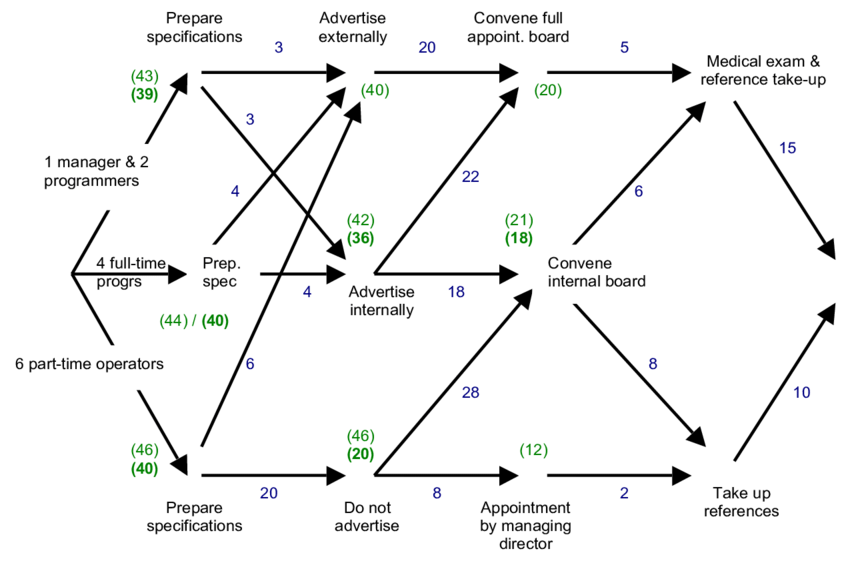
反向归纳法(Backward Induction):正向展望,反向推理。
首先,你需要思考自己的每个决策,以及对方在应对你的决策时,会采用何种决策。这个展开过程要一直推演到最后一步,此时你就可以看清双方在最后一步各自的最优选择;然后再反向回推到第一步。
反向归纳的前提是——你要获得充分的信息。
八、纳什均衡
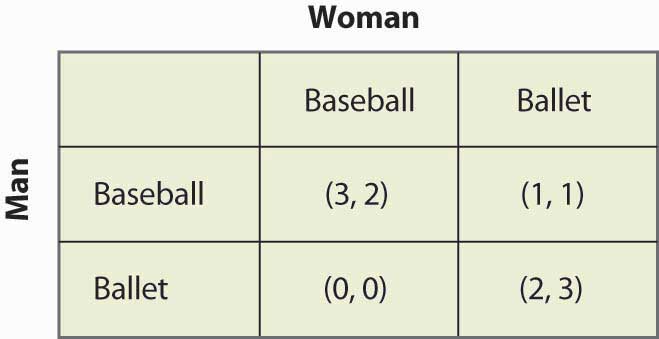
美国数学家纳什在1951年发表《非合作博弈》(Non-Cooperative Games),其中提出了纳什均衡(Nash Equilibrium)的概念并给出了相应的数学证明。
在多人的非合作博弈中,如果每个博弈者都无法单方面改善自己的境地,此时的局面称作纳什均衡。冯·诺伊曼已经在《博弈论与经济行为》一书中证明了:零和博弈必定存在这样的均衡点。
当博弈的局面处于纳什均衡,此时的系统是稳定的——如果每个博弈者都足够理性,他们都不愿意主动改变当前的策略。
九、博弈中的信息因素
Perfect Information和Imperfect Information
在顺序博弈过程中,如果每个参与者在做每个决策时,都能知道已经发生的每个事件的信息,称作Perfect Information;反之则是Imperfect Information。
大部分棋类游戏属于前者;某些军棋游戏(只能看到己方的棋子)和大部分扑克游戏属于后者。
Complete Information和Incomplete Information
如果每个博弈者的特征(如博弈目标、效用函数)都是公开的则称为Complete Information;反之是Incomplete Information。
几乎有所有的棋牌类游戏都属于Complete Information——双方的目标是公开且固定的(比如象棋的目标是干掉对方的王),而且也不用考虑“效用函数”之类的概念。
拍卖则属于Incomplete Information——有些人是真的买家,有些人只是为了抬价;即使是真正的买家,各自的底线也不公开。
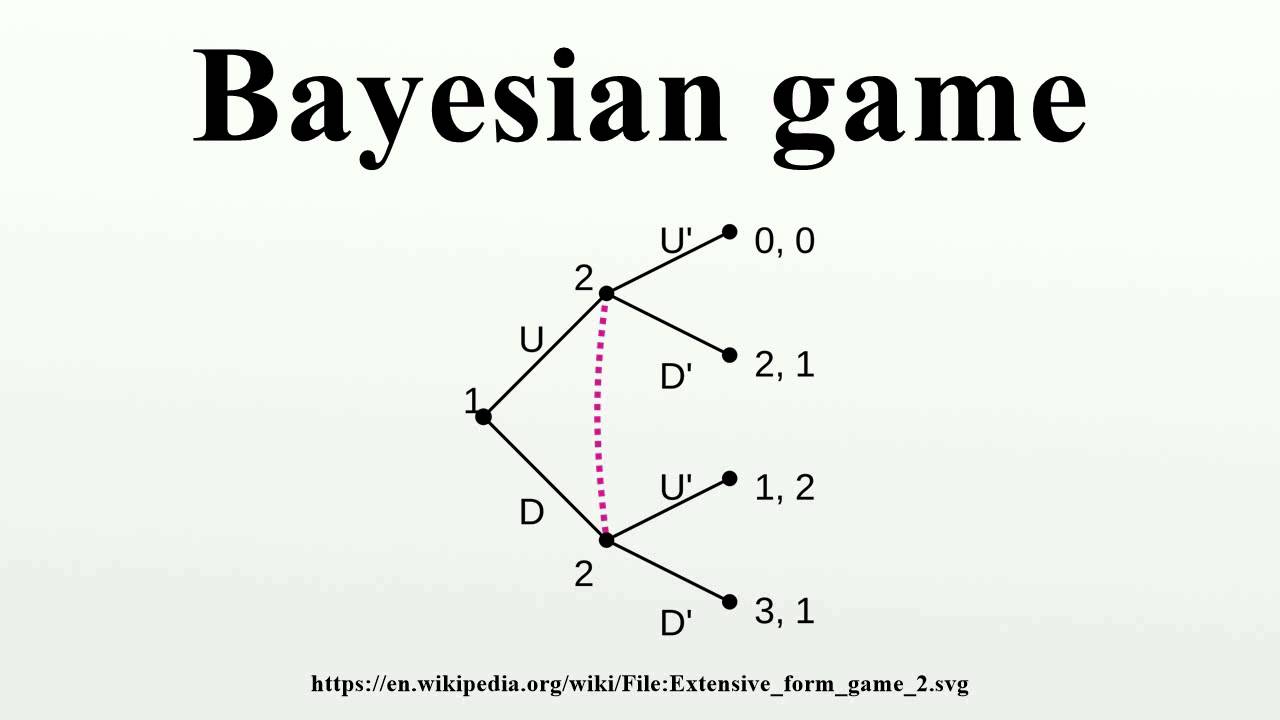
贝叶斯博弈(Bayesian Game)和贝叶斯纳什均衡(Bayesian Nash Equilibrium)
对于Incomplete Information的博弈,由于每个博弈者无法完全掌握其它博弈者的特征,需要引入贝叶斯定理(Bayes' Rule)进行概率分析,从而猜测其它对手的特征。所以这类博弈也称作贝叶斯博弈。对于贝叶斯博弈,其纳什均衡称之为贝叶斯纳什均衡(Bayesian Nash equilibrium,BNE)。
十、博弈中的心理因素
换位思考
你需要站在对手的角度进行思考,才能看清局面,从而更好地选择自己的策略。
理性人假设
早期微观经济学在进行数学建模的时候,通常都会引入一个理性人假设——假定市场的行为主体(公司或个人)是充分理性的。理性人假设基于幸存者偏见,常为平庸的大多数现象。
装疯策略
与理性人假设相反——理性的博弈者把自己伪装成非理性的博弈者,这么干可以获得某种虚张声势的唬人效果。

博弈论经典案例
- 同时博弈案例:囚徒困境,海盗分金
- 支配策略案例:美日新几内亚的航路作战
- 基于最小最大定理的顺序博弈案例:分蛋糕博弈
声明:本文大部分结构基于《博弈论入门教程——从基本概念到具体案例》一文速记,基于特殊原因恕不给出链接,感谢原作者。
👍
