每年的 3 月 14 日是圆周率日。在这一天，很多全世界的数学爱好者都会烘烤各种口味的馅饼(pie)以此来庆祝数学中最具代表性的无理数：π。毕竟 3.14 日是一年之中纪念这个重要数学常数的最佳时刻。

　　圆周率(π 或 Pi)是一个圆的周长与直径的比值。它作为无理数，它不能被表示为两个整数的分数，而是一个无穷无尽、永不重复的数。

　　圆的周长略大于其直径的三倍长。

　　但是这个无理数是如何被发现的？经过人们几千年的研究，这个数字还有其他什么秘密吗？从这个数字的古老起源，到它未知的神秘性质，这下面就是关于圆周率 π 的 10 个令人惊异的事实。

　　记忆背诵 π 的数位

　　据吉尼斯世界纪录记载，圆周率最多的记录属于印度韦洛尔的拉杰维尔·米纳，他在 2015 年 3 月 21 日花费了 9 小时 27 分钟内背诵了 7 万个圆周率的小数位。而此前的记录保持者，根据吉尼斯世界纪录，中国赵璐曾在 2005 年背诵到第 67890 位。

　　据英国《卫报》报道，还有一位非官方记录保持者，日本原口证（Akira Haraguchi），他在 2005 年录制了自己背诵圆周率小数点后 10 万位的视频，最近更是突破了 11.7 万位。

　　全球的数字爱好者们为了记住 π 的数位，会使用一些辅助记忆技巧手段，如被称为“π 学”的记忆技巧来辅助记忆。

　　“ 山巅一寺一壶酒（3.14159），尔乐苦煞吾（26535），把酒吃（897），酒杀尔（932），杀不死（384），乐尔乐（626）。”

　　而国外发烧友他们用 π 语写的诗（每个单词中的字母数对应一个 π 的数位），比如这段 π 文诗的节选：

　　How I want a drink, alcoholic of course, after the heavy lectures involving uantum mechanics.Now I fall, a tired suburbian in liuid under the trees,Drifting alongside forests simmering red in the twilight over Europe.（诗译：一堆量子力学讲座后，我想喝点什么，比如来点酒，我跌倒在树下，一个疲惫酒醉的乡下人，漂流在红树林旁，欧洲的暮色中。）（“How”单词有三个字符，“I”有一个，“want”有四个，依此类推。）

　　圆周率文字学的诞生

　　文学爱好者们发明了一种“π 语”，叫做 Pilish，这种语言类似上面记忆数位的技巧，连续单词中的字符个数与 π 数位一致。例如，迈克·基思（Mike Keith）的《Not A Wake》书中（2010 年，Vinculum Press 出版社）完全是用 π 语写成的：

　　Now I fall, a tired suburbian in liuid under the trees, Drifting alongside forests simmering red in the twilight over Europe.

　　可以利用这种方式来背诵 π，当然记忆大巨长的 π 的数位值时显然是缺乏效率。

　　人类认识 π 的程度呈指数增长

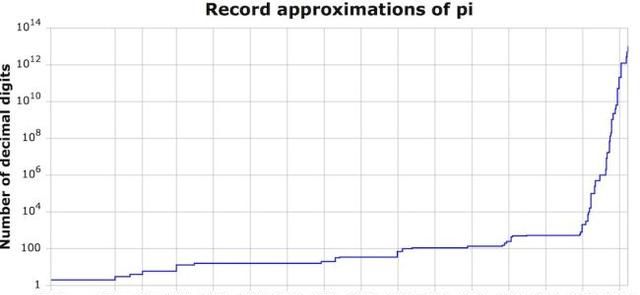
　　▲π的近似值记录时间轴图,注意垂直坐标使用了对数坐标。(图自维基)

　　圆周率是一个无限不循环小数，根据定义，人类永远也没法确定圆周率的所有位数。但是自 π 使用以来，数学家计算出来的小数位数确呈指数增长。

　　公元前 2000 年，巴比伦人认为分数 31/8 已经足够精细，而《旧约全书》似乎非常乐意使用整数 3 作为圆周率的近似值。公元 5 世纪时，南朝宋数学家祖冲之用几何方法将圆周率计算到小数点后 7 位数字。后来到了 1665 年，艾萨克·牛顿已经将 π 计算到小数点后 16 位。根据 1719 年，法国数学家托马斯·范泰德·拉尼计算出了 127 位小数，但遗憾是只有 112 位是正确的。

　　而计算机的出现，更是飞速提升了人类对 π 精度的认知。当数学家发现新的算法、电脑变得普及时，π的已知小数位急剧增加(如上面图形所示)。

　　根据《圆周率的历史》，1949 年至 1967 年间，圆周率的已知小数位数从 2037 猛增至巴黎 ENIAC 型计算机 CDC6600 得出的 50 万。而在 2019 年圆周率那天，谷歌工程师利用云计算更是计算到小数点后 31.4 万亿位，刷新了新的世界记录。

　　手算圆周率的方法

　　可以用最原始的方法计算圆周率，可以用一把尺子、一个圆罐和一根细绳、或者用一把圆规和一支铅笔来完成这项任务。用罐头法的缺点也很明显，首先我们需要是一个完美的圆形，还有能否准确围绕其周长绕一圈绳子也将直接影响其精确度。同样，用圆规画个圆，然后用尺子测量其直径或半径，也对准确和精度也需要较高挑战。

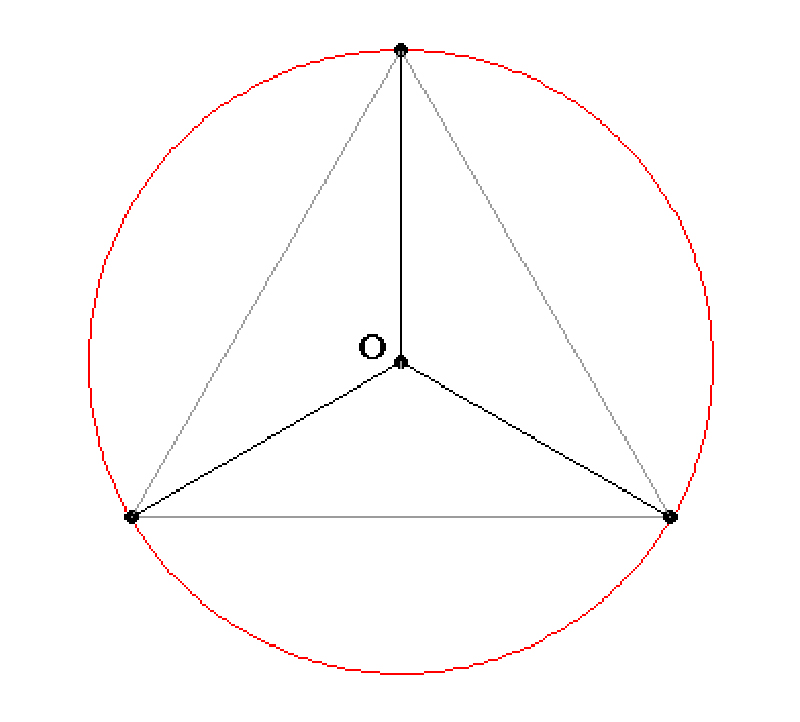
　　而更精确的选择是使用几何方法，比如割圆术。把一个圆分成多个部分（就像八片或十片切开的披萨一样）。然后，计算一条直线的长度，这条直线将把切片变成有两边相等的等腰三角形。加上所有的边对 π 产生粗略的近似。当分割的片段越多，对 π 的逼近就越精确。

　　π 的发现

　　最早有记载的对圆周率估值在古埃及和巴比伦，在 4000 年前，古巴比伦人就知道了 π 的存在。科学家发现一块公元前 1900 年到公元前 1680 年间的巴比伦泥板上显示出圆周率为 ，而公元前 1650 年，埃及的著名数学文献之一的莱因德数学纸草书上记录其值为 。

　　在《圣经》中对于 的近似值也这样描述过：&uot;他又铸一个铜海，样式是圆的，高五肘，径十肘，围三十肘。&uot; 其中肘就是用来估计 π 值的一个古老的长度单位，一肘相当于从手肘到中指尖的长度（估计大约 46 厘米）。

　　希腊数学家阿基米德（公元前 28—212 年）用圆内接多边形和相似圆外切多边形，当边数足够大时，两多边形的周长便一个由上，一个由下的趋近于圆周长。他先用六边形，以后逐次加倍边数，到了九十六边形，阿基米德计算出其面积，并且指出圆周率的值在 223/71<π<22/7。

　　我国数学家祖冲之(公元 429~500)利用某种近似的方法计算出了 的近似值是 。直到16世纪，阿拉伯数学家阿尔·卡西才打破了这一纪录。

　　π 符号的诞生

　　图自维基

　　在把符号 π 专指圆周率之前，数学家们不得不说一长串数值来代表它。据考古学家对古书的研究，在一本老书中发现了一个拉丁短语“uantitas in uam cum multiflicetur diameter, proveniet circumferencia”，意指“乘以直径可以等于周长的定量”，也就是圆周率 π 了。

　　而 π 第一次被提到是在一个鲜为人知的数学家威廉·琼斯（William Jones）的书中，他在 1706 年的《帕尔马里奥·马塞索斯概要》（Synopsis Palmariorum Matheseos）一书中使用了 希腊字母 π 代指圆周率。琼斯选用了 π 的原因可能是因为它是希腊文中“周边”一词“περιφρεια”的第一个字]。

　　巴塞尔问题是一个著名的数论问题，就是计算所有平方数的倒数和的准确值是什么，这个问题难倒了之前的数学家。1735年，伟大的瑞士数学家欧拉解决了，找到它与 π 的关系。

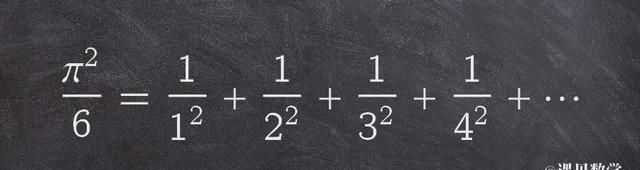
　　在 1736 年，欧拉在他的新书《力学》里用到的 π 这个符号，并且由于他频繁会与欧洲各国数学家通信往来讨论数学问题，其他数学家就纷纷接受这种用法，于是将 π 指代为圆周率传播开来，推广到整个世界。

　　π 是正规数吗？

　　尽管数学家已经揭开了这个无理数的许多谜团，但仍然有一些问题还等着人们进一步探索。比如，无穷无尽的 π 如此神秘，它属于正规数(Normal Number)吗？

　　截止目前为止，数学家仍然不知道圆周率是否属于所谓的正规数(即所有数字出现频率相同的数)，或者说这个数字中的 0 到 9 出现的概率是不是平均为 10%，而两位数值的任何组合(比如&uot;36&uot;)也平均为 1% 的概率出现。在 arXiv 杂志 2016 年 11 月 30 日出版的预印本上，Peter Trueb计算出，至少根据前 2.24 万亿的数字，数字 0 到 9 的频率表明 π 是正规数。这样基于实验证据，数学家猜想它很可能是正规数。当然考虑到 π 有无穷多个数字，唯一能证明这一点的方法就是给出严格的数学证明。

　　数学家们还在为此而努力，希望找到这个最著名无理数 π，以及另外一些无理数 √2、e、ln{2} 的证明，尽管他们已经对其数字的性质和分布取得了一些成果。

　　超越数

　　虽然科学家不知道圆周率是否正规数，但他们对圆周率的其他特性以已经有了。18世纪的数学家约翰·海因里希·兰伯特（JohannHeinrichLambert）利用的无穷连分数表达式证明了π是超越数(Transcendentalnumber)。

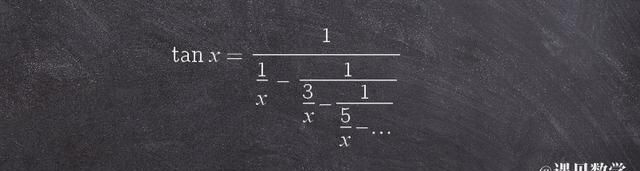
　　后来，数学家证明 π 也是超越数的。在数学术语中，超越数意味着这个数不能是任何有理数系数多项式的根。换句话说没有一个有限的、求根公式可以用有理数来计算出 π。

　　而超越数的证明，其实解决了几千年来数学上关于尺规作图三大难题，即倍立方问题、三等分任意角问题和化圆为方问题。随着超越数的发现，这三大问题被证明为不可能。

　　π 的危机

　　虽然许多数学爱好者对 π 很感兴趣，但另一种意见正在滋长。有人认为 π 是一个派生出来的常量，而 τ（等于 2π）其实是一个更直观好用的无理数。

　　图自:taoday.com

　　《Tau 宣言》的迈克尔·哈特尔（Michael Hartl）认为用 τ 能将很多数学、物理上的公式简化，使得变得更加优雅。比如，直接能将周长与半径联系起来，而半径在数学上是一个更重要的值。

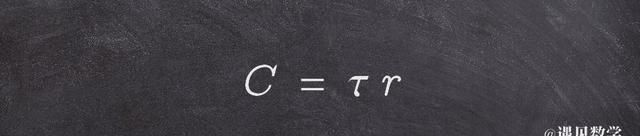
　　当然，τ 在三角计算中也有简化的效果，例如， 弧度对应于刚好扫过四分之一圆的角度。

　　在国际数学日庆祝 π 日！

　　1988 年，物理学家赖瑞·萧在旧金山探险家科学博物馆举办了首次圆周率派对，然后每年的这天，那里的工作人员和游客们都举着 π 的某位数值在那里举行一次环形游行，活动里当然免不了还要品尝下美味的馅饼。

　　▲ 赖瑞·萧及 Pi Day 的环形游行

　　在 2019 年联合国教科文组织第四十届大会上正式宣布每年的 3 月 14 日是“国际数学日”，相信在这个特殊的日子里开展纪念和庆祝活动会让学子欣赏数学，它在我们日常生活中的美丽，作为理解世界的运作和探索未来不可或缺的重要工具，而计算更精确的 π 值的追求也永远在路上。