你可能早已听说过，π 与地球上的许多河流有关：河流弯曲河道的曲线长度与河道首尾直线距离之比通常都接近于 3.14 —— 河道越是蜿蜒曲折，这个近似值就越好——亚马逊河便是一个例子。
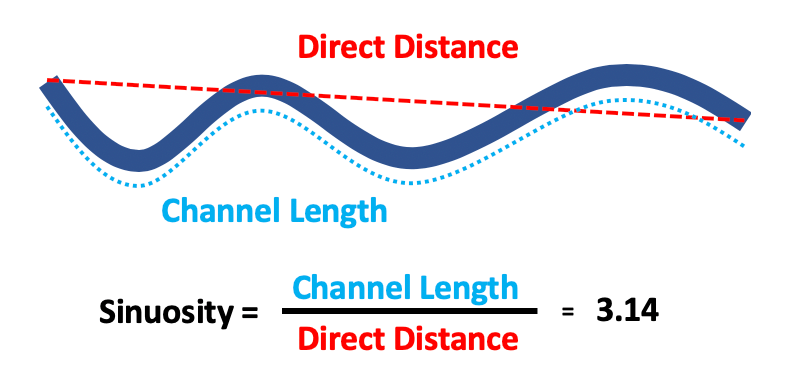
https://envirobites.org/2019/03/14/pi-me-a-river-a-meandering-tale-of-pi-rivers-and-water-quality/
最令我惊叹的是 2010 年 11 月 《科学》杂志上报道的德国格丁根大学马克 · 普朗克动力学与自组织科学研究所和伯恩斯坦计算神经科学研究中心的科学家 Matthias Kaschube 及其团队的一项研究成果。
圆周率 π 是一个不等于任何两个整数之比的实数，它在整数 3 之后再 带上一个具有无限长度但又永远不循环的小数：π ≈ 3.1415926 · · · 。尽管人类对 π 的认知可以追溯到远古，最先对 π 值进行系统严格的估算者应当首推古希腊科学家 Archimedes（阿基米德，公元前 287—前 212 年），他得出不等式 3 + 10/71 < π < 3 + 1/7，平均值就是 π ≈ 3.14 · · · 。
祖冲之（429-500）
在我国，三国后期魏国人刘徽（生于公元 250 年左右）留下了宝贵数学遗产《九章算术注》和《海岛算经》，并创始和使用了“割圆术”即用圆的内接和外切正多边形来逼近圆的周长。割圆术为后来南北朝时期的数学家祖冲之（公元 429—500 年）的估算 3.1415926 < π < 3.1415927 提供了最基本的方法。此外，祖冲之还以很简单的分数形式给出了圆周率的约率 π ≈ 22/7 和密率 π ≈ 355/113。
在最初的《星际迷航》中，斯波克先生（已故的伟大犹太人演员伦纳德·尼莫伊饰演）指挥一台邪恶的计算机，该计算机接管了星舰企业的生命支持系统，将Pi计算到最后一位。因此，Spock胜过了致命的半机械人，后者毁了自我毁灭，因为正如Spock解释的那样，“ Pi的价值是无法解决的先验人物”。Spock完全合乎逻辑，并不是在暗示Pi具有某种超越的精神品质。相反，先验是一个数学术语，我将为您省去定义，希望您能继续阅读本段以外的内容。但是尽管有Spock和他的逻辑，Pi可能仍然具有超越的精神品质。
圆的周长始终为直径的3.14 x。除了3.14（我们现在称为Pi）之外，只是一个近似值。小数实际上一直在流动。Pi不仅是一个无理数，而且是无限的，最终是不可知的。然而，尽管数字本身总是在逃避我们的掌握，但我们也知道，它总是真实且始终可靠的。Pi始终表示圆的直径和周长之间的数学关系，而不管圆是多小或多大。
3月14 日和 7 月22 日密切相关。这些是Pi日和Pi近似日，基于上面的月/日和日/月格式中的数字表示。每天的Pi日，数学家都会被要求写这样的文章，有些人背诵π的数字，而另一些人则以这一天为借口，尽可能多地吃馅饼。
但是为什么π对数学家和数学生物学家很重要？
